January 8, 2014 by ibrivio

What is a neutrino?

Neutrinos are elementary subatomic particles, just as electrons and quarks. They are special because of two main reasons: their mass is super-tiny and they show a certain reluctance to interact with the rest of matter. Actually, the mass of neutrinos hasn't been measured exactly yet, but we know that it takes at least 500000 of these small particles to reach the mass of an electron, and one billion for the mass of a proton! F. Reines described them as "...the most tiny quantity of reality ever imagined by a human being".

As we said, neutrinos are also quite elusive particles. This happens because among the four fundamental interactions existing in Nature, neutrinos only participate to two: the gravitational one and the weak one. The former has practically no role in particle physics, due to the smallness of the masses in play. The latter, as its name suggests, is considerably weaker than the electromagnetic and strong forces. As a result, neutrinos practically travel straight through matter, as they don't "see" any obstacle in it!

Where do they come from?

The weak interaction is the one that makes radioactive decays possible: it is the only one capable of transforming a neutron into a proton. Every time this happens, an electron must be emitted together with a neutrino, and this is basically the way neutrinos are produced in nature.

This kind of processes are massively present, for example, in the nucleus of the Sun: our star shines mainly thanks to the thermonuclear fusion of hydrogen nuclei into helium taking place there. For each ⁴He nucleus produced, two neutrinos are emitted, so that the Sun indeed represents our main source of neutrinos nowadays. However, the majority of the neutrinos floating around were born already a few instants after the Big Bang, and since then they just kept going! It is estimated that there are 30 millions of such neutrinos in each cubic meter of the Universe, which also makes them the most abundant particle specie in the Universe. There are so many cosmic neutrinos that they're said to constitute a cosmic background! Another important, but yet exceptional, source are supernova explosions: in some special conditions, the life of a star ends with a spectacular explosion and the release of a huge amount of energy, of which about the 99% is in form of neutrinos. Finally, a smaller but significant number of neutrinos are also continuously produced at nuclear reactors, or in the decay of particles present in the atmosphere

"Neutrinography" of the Sun ralized by SuperKamiokande, i.e. the sun as seen detecting its neutrino emission.
Source: http://www-sk.icrr.u-tokyo.ac.jp/sk/physics/solarnu-intro-e.html

Why are neutrinos so interesting? What can they tell us?

There are many reasons why physicsts love neutrinos: in fact this shy particles could give us precious information to help us solve a number of problems in particle physics.

For example, one of the most important and obscure facts in our present knowledge of the particle's world is that all the basic constituents of matter come in three different types, called flavors. We have found three positively charged quarks, called up (u), charm (c) and top (t), three negatively charged ones, called down (d), strange (s) and bottom (b) and, again, three copies of the electron: itself (e), the muon (μ) and the tau (τ). Indeed, we also have three types of neutrino: a ν_e, which is always produced together with an electron, a ν_μ and a ντ produced with the μ and the τ respectively. The three flavor families appear ordered hierarchically: the mass of the top quark is about 100 times bigger than that of the charm, which in turn is some 1000 times heavier than the top. Similar patterns exist also among the triplets (d, s, b) and (e, μ, τ).

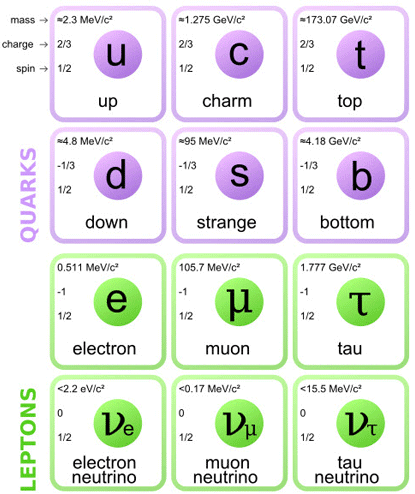
Scheme of the three generations of matter constituents observed in Nature.

This looks peculiar, but still we have no idea of how and why this happens! Why are there three copies of everything? Why are they ordered this way and why are the masses of the particles span such a wide range? No answer, for the moment. But neutrinos can provide a decisive clue to solve this puzzle. Why? Well, mainly because they show an incredible ability to, literally, transform into one another! It is quite common, indeed, to produce a ν_μ and find, after a while, that it has become a ν_τ ! This phenomenon can take place among any two flavor pairs and the probability for it to happen is periodical, so that it is called neutrino oscillation. This particular ability of neutrinos is the most eloquent signal we have of any relation existing among the three flavors, and understanding it would mean making huge progress in the solution of the flavor puzzle.

There are also cosmological reasons pushing to chase after neutrinos: as we said before, most of the neutrinos in the Universe were produced just after the Big Bang. As the Universe expanded, then, they just continued their journey cooling down slowly, but without undergoing any interaction for billion years. Therefore, the information they carry may provide unique insights to the epoch in which they were produced, helping us to answer questions about the age of the Universe, its expansion rate and composition in its very first seconds. Did accelerate at some point? How may photons were there? What was the temperature at that time?... and many others!

Going on, we could list many other enigmas that the study of neutrino properties could illuminate, including why Nature is made out of matter and not of antimatter (all the same particles with charged of opposite sign), or what is there beyond the particles we have seen so far.

How do neutrinos oscillate?!

Neutrino oscillations are the phenomenon by which a neutrino born of a certain flavor can be found, after some time, to have "transformed" into one of another family. The word "oscillation" just indicates that the probability for this to happen is periodical.

Neutrino oscillations are a typical quantum mechanical effect: according to Quantum Mechanics, in fact, each particle can be seen also as a wave. We can think that every kind of particle is described by a wave with a peculiar shape. In general, these waves will be the superposition of different components, pretty much as sea waves never happen to be perfectly sinusoidal. Let's take for example ν^e and ν_μ and let's say that each of them corresponds to a different combination of two components, that we may call ν₁ and ν₂.

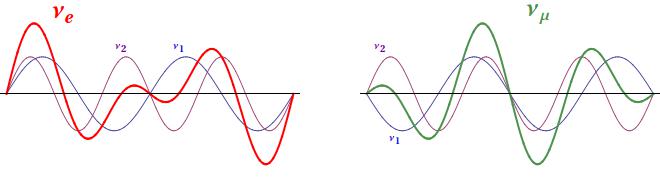
How do the ν_e and ν_μ packets propagate in space? Well, it depends on what ν₁ and ν₂ do! If the velocities of ν₁ and ν₂ are the same, also νe and νμ propagate at the same speed without changing their shape. If the velocities of ν₁ and ν₂ are different, however, their superposition changes periodically! Thus, after some time, the "νe shape" gets transformed into the "ν_μ shape" and, if we detected the neutrino in this instant, we would find that its flavor has simply transformed! In the example here below, ν₁ is two times quicker than ν₂:

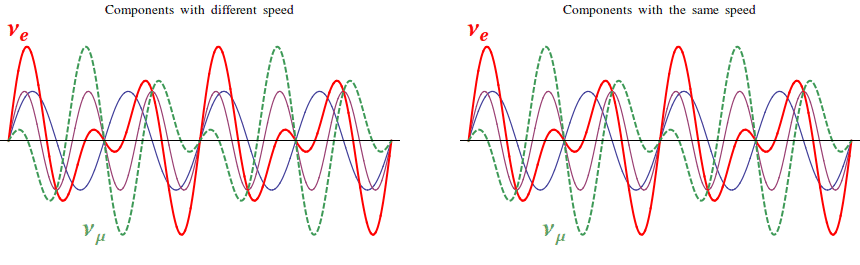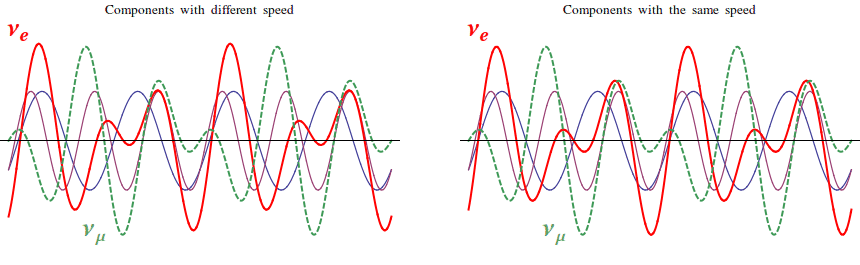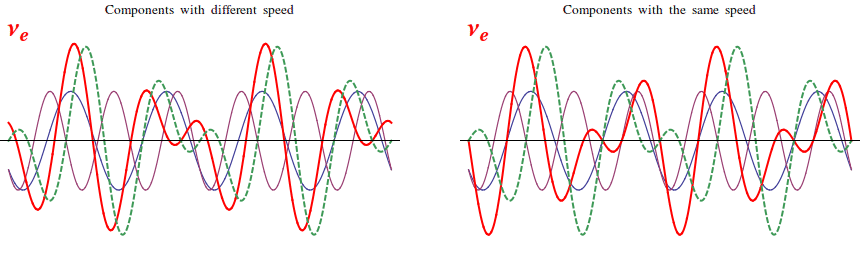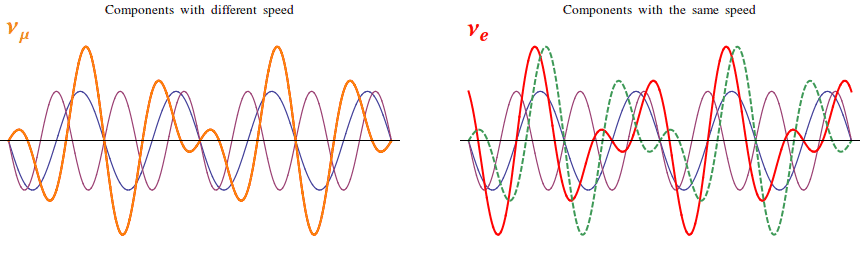
What does this simple example mean, physically? The components ν₁ and ν₂ have definite speed, which means that they represent a particle with definite mass. When one is slower than the other, it is because it is heavier, while if their velocities are equal, they have the same weight. The waves ν_e and ν_μ, instead, are characterized by a definite flavor, i.e. they represent the particles that are produced with the electron and with the μ in radioactive decays. So, quantum mechanics tells us that neutrinos with a definite flavor are combination of neutrinos with a definite mass! If this sounds weird and hard to understand, don't worry: most of the physicists struggled to understand and accept the quantum theory for years after its formulation in the 20s!

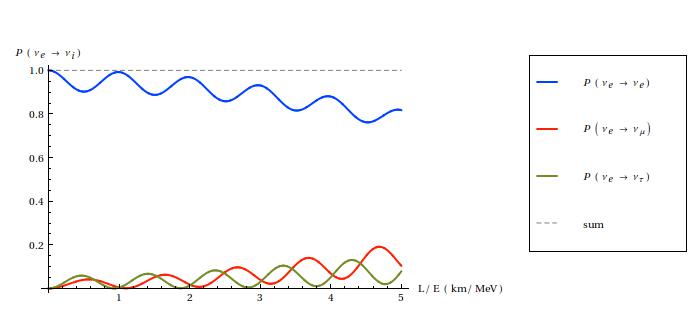
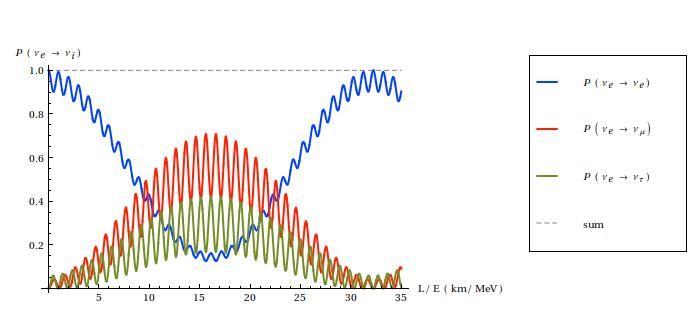
The essence of neutrino oscillations is that ν_e, ν_μ and ν_τ may transform into one another during their path, and that this happens because the three types of neutrinos have different masses. Indeed, this is how we know that at least two of them must be massive (only the differences count, so we don't have information about the lightest). It is possible to calculate the probability with which an electron neutrino, for example, can be found to have converted into a muon one. The result is expressed by quite a complicated formula, and is a function of the ratio L / E, i.e. distance (L) over the energy (E) of the neutrino. Here below you can see two plots for each flavor of the initial neutrino: a "short distance" behavior and a broader overview. Say that you pick, for example, "ν_e" and you want to know what is the probability to find that this neutrino has become a ν_μ after 10 km, assuming that its initial energy was of 10 MeV. Then your L/E is 1 km/MeV, and the red line in the first diagram tells you that that probability is practically zero. So to what distance should you place your detector in order to have a sensible chance to see the oscillation effect? Well, for example, you see from the second plot that the red line is quite high for L/E around 15 km/MeV, which means that if you stay roughly at a distance L = 15 ⋅ 10 = 150 km, then you would have a 50-70 % of chances to see a ν_μ!

Oscillation probabilities at short and long distances for an initial electron neutrino

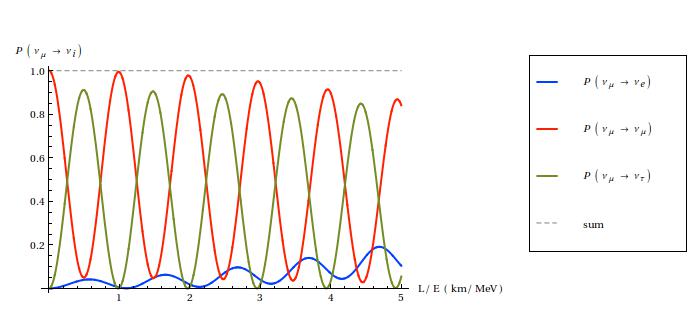
Oscillation probabilities at short and long distances for an initial muon neutrino

Oscillation probabilities at short and long distances for an initial tau neutrino

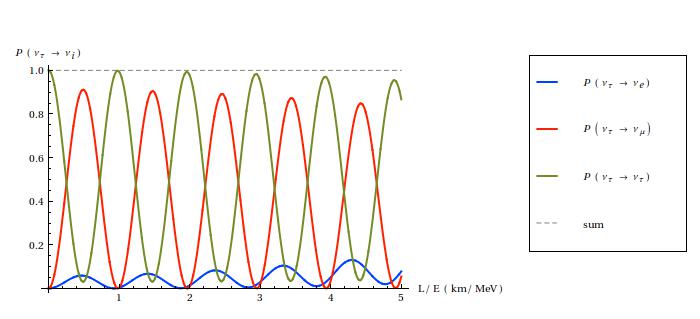
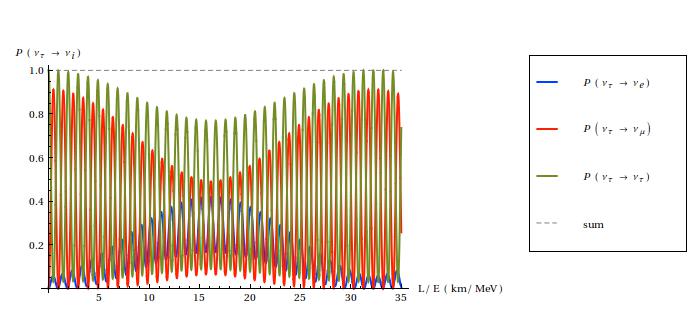
Oscillation probabilities at short and long distances for an initial tau neutrino

What can we do with this? What can oscillations tell us about neutrinos?

In the last twenty years many neutrino oscillation experiments have been constructed all over the world: the oscillation phenomenon is indeed the only direct window we have on the flavor structure of neutrinos, and perhaps also on that of all the other particles. This structure is described mathematically by a matrix with four parameters, whose exact values, if known, would provide crucial indications for the solution of the flavor puzzle. Nowadays, three of these parameters (called mixing angles) are known, even though the accuracy of their measurements is still unsatisfactory. On the fourth (named CP phase ) we still don't even have a clue.

As we said, the way we access these fundamental parameters is through neutrino oscillations: what physicists do is to pick a neutrino source that emits a know neutrino flux (e.g. the sun, the atmosphere or a nuclear reactor), and place a neutrino detector at some fixed distance from it, in order to measure how the composition of the flux has changed along the path. The measured oscillation rate can be expressed with a formula that depends on the four mixing parameters, the three neutrino masses, the initial neutrino energy and the source-detector distance. Thus, knowing all the other quantities, it is possible to extrapolate from the measurement the value of one of the parameters we're interested in. What happens is that we have many unkown parameters (seven!) and that each experiment, depending on its caracteristics, is typically sensitive only to one or two of these. So this is why many experiments of different kind are needed to obtain a complete picture.

It is especially challenging to build an efficient neutrino detector: huge volumes of material (typically water) are needed in order to amplify the probability that a neutrino interacts with it and, moreover, very though screens are needed against a lot of other phenomena that would obscure the feeble neutrino signal. Most of these backgrounds are due to cosmic rays or to reactions taking place in the atmosphere, and therefore all neutrino experiments must be located deep undergound, under mountains or inside old caves, so as to put a kilometric layer of rock between the atmosphere and the detector. So, the first experiment to give evidence for neutrino oscillations was SuperKamiokande, in 1998. This experiment is located 1000m underground, in the Mozumi mine under Mount Kamioka in Japan, and its famous detector consists in a cylindrical stainless steel tank that is 41.4 m (136 ft) tall and 39.3 m (129 ft) in diameter holding 50000 tons of ultra-pure water. All of the tank's surface is covered with photomultipliers, a special kind of detectors able to see the signal emitted by the captured neutrino. SuperKamiokande observed neutrinos produced in the atmosphere, observing a lack of ν_μ's in the flux, compensated by an excess of ν_e's, which constituted the first undeniable proof that neutrinos do change their flavor and provided the first estimate for the difference m32-m22≈ 2.4 ⋅10 -3 eV2. A confirmation of this same kind of oscillation was provided in 2004 by the K2K experiment, in which the SuperKamiokande detector observed neutrinos sent from the KEK particle accelerator, located at a distance of about 250km. More recently, the same "atmospheric parameters" have been measured with much higher accuracy by MINOS, an experiment started in 2005 that analyzed neutrinos produced at the NuMI facility at Fermilab, and by T2K, the currently active successor of K2K.

The SuperKamiokande water tank during its filling. The walls are entirely covered with photomultipliers.

Other experiments focused instead on solar neutrinos: SNO, for example, obtained the first evidence for oscillations of neutrinos coming from the sun in 2002. An independent proof for the same kind of transition came in the same year from the KamLAND experiment, that analyzed the neutrinos produced by 55 reactors in Japan at an average distance of 180km. This led to the measure of the second mass difference m₂²-m₂²≈ 7.3 ⋅ 10 ^_-5 eV².

Finally, the Chooz and Double Chooz experiments in France, as well as Daya Bay in China and RENO in South Korea, focus on another special mixing parameter, the angle θ_e3 which was long believed to be exactly zero. To have a null quantity in the mixings would have been a very peculiar fact, an indication towards a very special flavor structure of nature. However, the most recent results from Daya Bay, RENO (2012) and T2K (2013) show in a more and more convincing way that this angle is not zero at all, but rather around 10°.

These are only a sample of all the neutrino oscillation experiments ever built. In the map below (which is still inexhaustive) you can locate more of them and look for more details about each.